2062 Kraftkomposant och resultant

Kraft betecknas med F.

Enheten för kraft är newton [N].

Kraftkomposant

Vid problemlösning kan det finnas behov av att dela upp en kraft i två krafter.

En kraft F se figuren ovan och nedan, kan delas upp i komposanter F_x och F_y, se figur nedan.

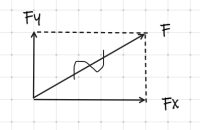
Koordinatform

Krafter kan skrivas på koordinatform. Om en ruta motsvarar 1 N kan krafterna skrivas som:

F = (5, 3)

F_x = (5, 0)

F_y = (0, 3)

Kom ihåg att koordinater skrivs som (x, y), där x är åt höger och y är uppåt.

Det går att lägga ihop koordinaterna för F_x och F_y och få koordinaten för F.

(5, 0) (0, 3) +______ =(5, 3)

Kraftresultant

Om man har två krafter kan det vid problemlösning finnas behov av att ersätta dem med en kraft.

Kraften F ovan kallas resultant till krafterna F_x och F_y.

Fler sätt

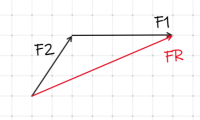
Två krafter F₁ och F₂ visas nedan.

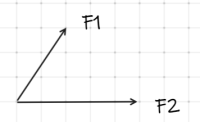
Krafterna kan läggas ihop genom att pilen F₂ läggs efter pilen F₁, se figur nedan. Kraftresultanten betecknas med F_R.

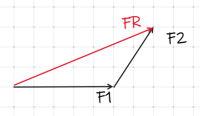
Eller så kan krafterna läggas ihop i omvänd ordning, se figur nedan.

Koordinatform

Krafter kan också adderas som koordinater.

Om en ruta är 1 N blir koordinatformerna som följer:

F₁ = (2, 3)

F₂ = (5, 0)

Kom ihåg att koordinater anges som (x, y), där x är på den liggande axeln och y är i riktningen uppåt.

Kraftresultanten F_R fås då med följande addition:

(2, 3) (5, 0) +_____ =(7, 3)

Kontroll i någon av figurerna nedan ger att F_R kan skrivas som (7, 3)

Känt från matematiken

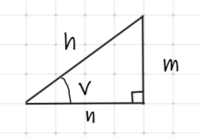
Kort förklaring av beckningarna i figuren ovan.

v - vinkel

n - närliggande katet till vinkeln

m - motstående katet till vinkeln

h - hypotenusan

Pytagoras sats:

h² = n² + m²

Trigonometri

sin(v) = m/h

cos(v) = n/h

tan(v) = m/n

Inversa triogonometriska funktioner:

v = arcsin(m/h)

v = arccos(n/h)

v = arctan( m/n)

eller med annat skrivsätt:

v = sin^-1(m/h)

v = cos^-1(n/h)

v = tan^-1(m/h)

Nyttan av ovanstående matematik i fysik

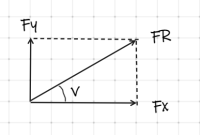
F_R känd

Vill dela upp i komposanterna: F_x och F_y.

F_x = F_Rcos(v)

F_y = F_Rsin(v)

F_x och F_y

Vill räkna ut kraftresultanten F_R och vinkeln v.

Pythagoras sats ger:

F_R² = F_x² + F_y²

Ta roten ur på båda sidorna eller upphöj båda sidorna till 1/2. Det medför:

F_R =( F_x² + F_y²)^1/2

Vinkeln fås på följande vis:

v = arctan( F_y/ F_x)

eller med annat skrivsätt:

v = tan^-1( F_y/ F_x)